The donuts code & the math behind

Published on 31 January 2021 12:00 AM
#c #Math

The Donuts Code

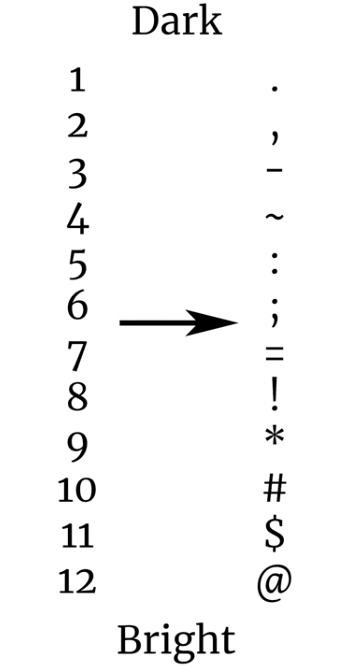
The spinning "donuts" that has brought some attention recently and was created by the amazing Andy Sloane. No wonder, a flying donut on your terminal? You can find the code below in c. The "pixels" are ASCII characters .,-~:;=!*#$@ that accounts for the illumination value of the surface, but I'll explain step by step below along with the math.

Mission: 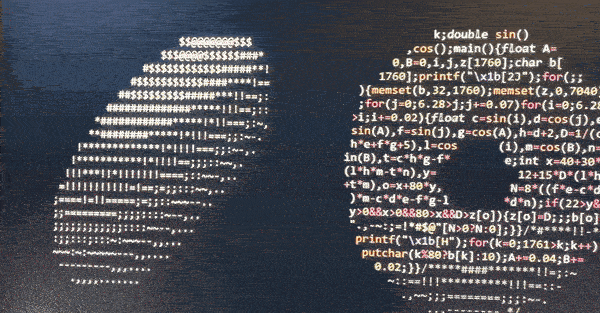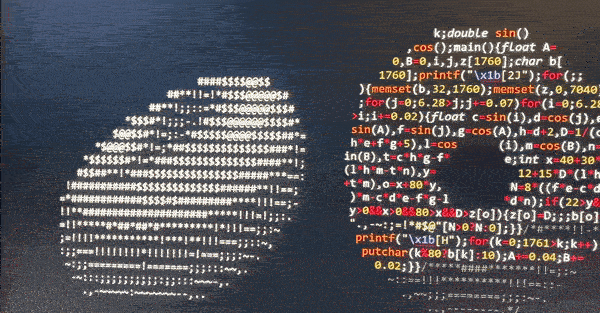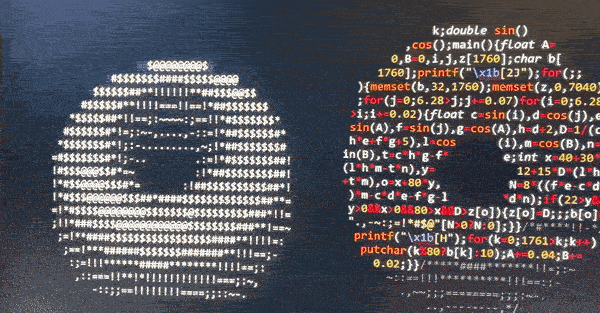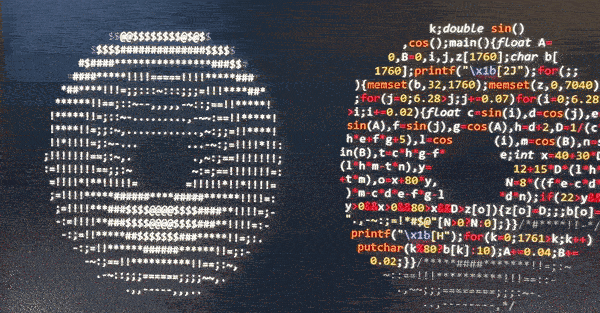png

Steps

  1. Create a circle of radius R2 centred at R2 png

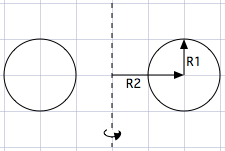
  2. Create a torus('donuts') which rotates on the Y axis png

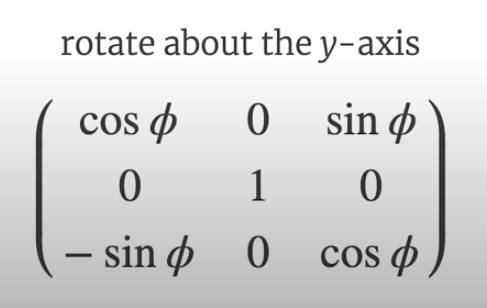
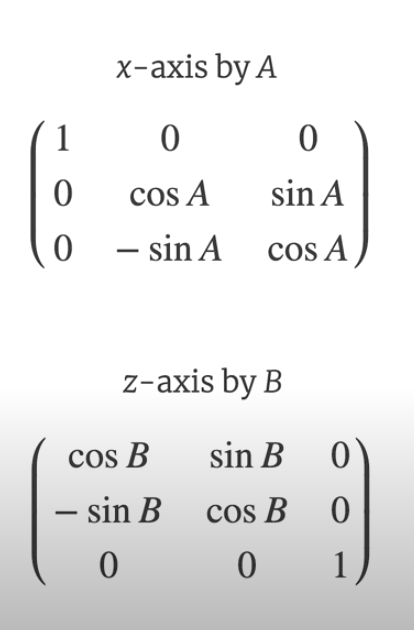
  3. Now, we need to rotate about the X and Z axis so it looks like it's floating and spinning on the screen. Basically, a flying donut. Why not? png

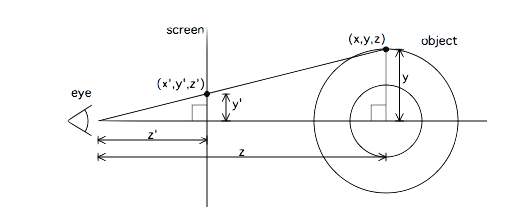
  4. Well, how to map this 3D objet into 2D ie terminal screen? png

Each character in the code corresponds to a pixel on our terminal. However, how to shade it? For this, we calculate the dot product of the surface normal and the direction of the light. This will say how light and how dark will look on the screen.

png

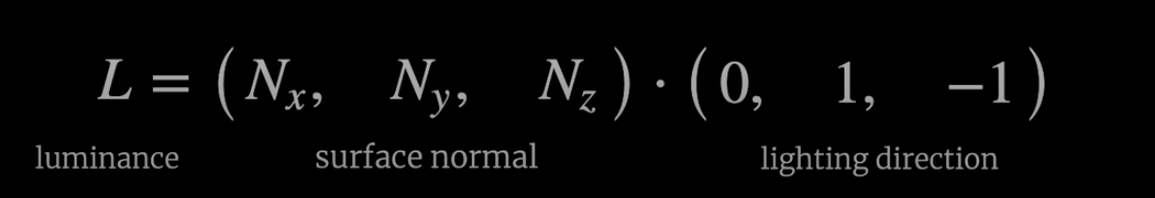
The output of the dot product will be: 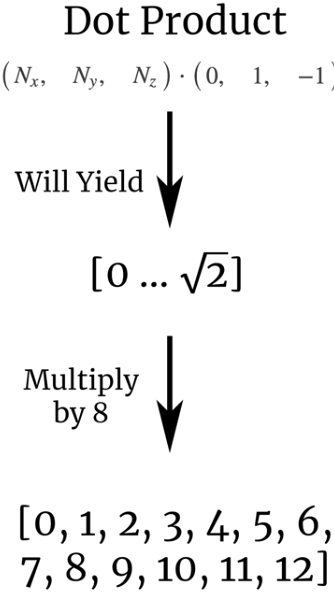png

  1. Finally you map the result of the dot product (step 4) to these characters to tweak the lighting. That's it! png
    png
Code
#include <stdio.h>
#include <math.h>
#include <string.h>
#include <unistd.h>

int main() {
    float A = 0, B = 0;
    float i, j;
    int k;
    float z[1760];
    char b[1760];
    printf("\x1b[2J");
    for(;;) {
        memset(b,32,1760);
        memset(z,0,7040);
        for(j=0; j < 6.28; j += 0.07) {
            for(i=0; i < 6.28; i += 0.02) {
                float c = sin(i);
                float d = cos(j);
                float e = sin(A);
                float f = sin(j);
                float g = cos(A);
                float h = d + 2;
                float D = 1 / (c * h * e + f * g + 5);
                float l = cos(i);
                float m = cos(B);
                float n = sin(B);
                float t = c * h * g - f * e;
                int x = 40 + 30 * D * (l * h * m - t * n);
                int y= 12 + 15 * D * (l * h * n + t * m);
                int o = x + 80 * y;
                int N = 8 * ((f * e - c * d * g) * m - c * d * e - f * g - l * d * n);
                if(22 > y && y > 0 && x > 0 && 80 > x && D > z[o]) {
                    z[o] = D;
                    b[o] = ".,-~:;=!*#$@"[N > 0 ? N : 0];
                }
            }
        }
        printf("\x1b[H");
        for(k = 0; k < 1761; k++) {
            putchar(k % 80 ? b[k] : 10);
            A += 0.00004;
            B += 0.00002;
        }
        usleep(30000);
    }
    return 0;
}

Credits